练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图是一个空间几何体的主视图、侧视图、俯视图，如果主视图、侧视图所对应的三角形皆为边长为2的正三角形，俯视图对应的四边形为正方形，那么这个几何体的体积为              ．

    试题分析：因为题目中给定了主视图、侧视图所对应的三角形皆为边长为2的正三角形，俯视图对应的四边形为正方形，则说明那个该几何体是四棱锥，底面正方形，高为，那么利用四棱锥的体积公式,故答案为
    点评：关键是利用三视图还原几何体，然后借助于锥体的体积公式来求解得到。三视图的最重要的一点就是俯视图，能确定原几何体中的底面形状，，属于基础题。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    圆柱的一个底面积为4π，侧面展开图是一个正方形，那么这个圆柱的侧面积是          

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知球的某截面的面积为16，球心到该截面的距离为3，则球的表面积为         .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    两个球的体积之比为，那么这两个球的表面积的比为          ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若某多面体的三视图（单位：cm）如图所示,则此多面体的体积是（    ）

    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知满足，若的最大值为，最小值为，则a的范围为     （ ）
    A．B．C．D．或

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

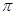    半径为r的圆的面积S(r)＝r2,周长C(r)=2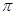r，若将r看作(0，＋∞)上的变量，则(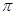r2)`＝2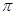r ①，①式可以用语言叙述为：圆的面积函数的导数等于圆的周长函数。对于半径为R的球，若将R看作(0，＋∞)上的变量，类比以上结论，请你写出类似于①的式子：            ②，②式可以用语言叙述为：                           。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

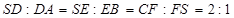    一个盛满水的三棱锥容器，如图所示，不久发现三个侧棱上各有一个小洞D，E，F。且知，若仍用该容器盛水，最多盛水（可以任意情形放置）为原三棱锥体积的（   ）
    A．B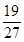．C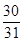．D．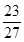

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为
    A．3pa2B．6pa2 C．12pa2D．24pa2

    查看答案和解析>>

    同步练习册答案