
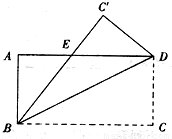
 如图,把长方形ABCD沿BD对折,使C点落在C′的位置时,BC′与AD交于E,若AB=6cm,BC=8cm,求重叠部分△BED的面积.
如图,把长方形ABCD沿BD对折,使C点落在C′的位置时,BC′与AD交于E,若AB=6cm,BC=8cm,求重叠部分△BED的面积. 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
| 2 |
| π |
| 2 |

| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省高三三模考试文科数学试卷(解析版) 题型:解答题
如图,已知长方形ABCD中,AB=2,A1,B1分别是AD,BC边上的点,且AA1=BB1="1," E,F分别为B1D与AB的中点. 把长方形ABCD沿直线 折成直角二面角,且
折成直角二面角,且 .
.

(1)求证:
(2)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:揭阳二模 题型:解答题
| 2 |
| π |
| 2 |
| ||
| 2 |
查看答案和解析>>
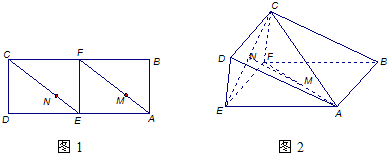
科目:高中数学 来源:2006-2007学年浙江省台州市临海市高二(下)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com