
| A. | 关于点($\frac{5π}{12}$,0)对称 | B. | 关于点($\frac{π}{2}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
分析 写出函数的对称轴和对称中心,逐个选项验证可得.
解答 解:由2x+$\frac{π}{6}$=kπ可得x=$\frac{kπ}{2}$-$\frac{π}{12}$,故函数的对称中心为($\frac{kπ}{2}$-$\frac{π}{12}$,0),k∈Z,
当k=1时,可得其中一个对称中心为($\frac{5π}{12}$,0),故A正确;
令$\frac{kπ}{2}$-$\frac{π}{12}$=$\frac{π}{2}$可得k=$\frac{7}{6}$∉Z,故B错误;
由2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$可得x=$\frac{kπ}{2}$+$\frac{π}{6}$,故函数的对称轴为x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
令$\frac{kπ}{2}$+$\frac{π}{6}$=$\frac{5π}{12}$可得k=$\frac{1}{2}$∉Z,故C错误;
令$\frac{kπ}{2}$+$\frac{π}{6}$=$\frac{π}{12}$可得k=-$\frac{1}{6}$∉Z,故D错误.
故选:A
点评 本题考查正弦函数图象的对称性,属基础题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
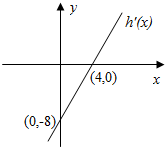 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com