
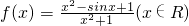 存在最大值M和最小值N,则M+N的值为________.
存在最大值M和最小值N,则M+N的值为________. ,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数,
,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数, =1-
=1- ,令g(x)=-
,令g(x)=- ,则有f(x)=1+g(x),且g(x)是奇函数.
,则有f(x)=1+g(x),且g(x)是奇函数.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com