练习册

  • 练习册
  • 试题
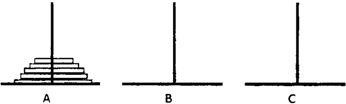    精英家教网 > 高中数学 > 题目详情
    9、有三根杆子A，B，C，A杆上串有3个穿孔圆盘，尺寸由下到上依次变小，要求按如下规则将圆盘移至C杆上：（1）每次只能移动一个盘子；（2）在每根杆子上始终保持大盘在下小盘在上的次序，则需移动盘子最少（　　）次．
    分析：根据题意，从A杆移到C杆上分七步，即A→C，A→B，C→B，A→C，B→A，B→C，A→C，有七种方法，即需移动盘子最少7次．
    解答：解：将圆盘移至C杆上：（1）每次只能移动一个盘子；（2）在每根杆子上始终保持大盘在下小盘在上的次序，方法如下：从A杆移到C杆上分七步，即A→C，A→B，C→B，A→C，B→A，B→C，A→C，有七种方法，
    则需移动盘子最少7次；
    故选B．
    点评：本题考查了数列知识和归纳推理应用，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网汉诺塔问题是根据一个传说形成的一个问题：有三根杆子和套在一根杆子上的若干大小不等的穿孔圆盘，按下列规则，把圆盘从一根杆子上全部移到另一根杆子上．
    ①每次只能移动1个碟片；②大盘不能叠在小盘上面．
    如图所示，将A杆上所有碟片移到C杆上，B杆可以作为过渡杆使用，称将碟片从一个杆子移动到另一个标子为移动一次，记将A杆子上的n个碟片移动到C杆上最少需要移动an次．
    （Ⅰ）写出a1，a2，a3，a4的值；
    （Ⅱ）求数列{an}的通项公式；
    （Ⅲ）设bn=
    nan+1
    ，求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    汉诺塔问题是指有三根杆子和套在一根杆子上的若干大小不等的碟片，按下列规则，把碟片从一根杆子上全部移到另一根杆子上：（1）每次只能移动1个碟片；（2）较大的碟片不能放在较小的碟片上面．
    如图所示，将B杆上所有碟片移到A杆上，C杆可以作为过渡杆使用，称将碟片从一根杆子移动到另一根杆子为移动一次，记将B杆子上的n个碟片移动到A杆上最少需要移动an次．
    （1）写出a1，a2，a3，a4的值；
    （2）求数列{an}的通项公式；
    （3）设bn=
    1
    an+1
    +
    1
    anan+1
    ，数列{bn}的前n项和为Sn，证明
    2
    3
    ≤Sn＜1    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    有三根杆子A，B，C，A杆上串有3个穿孔圆盘，尺寸由下到上依次变小，要求按如下规则将圆盘移至C杆上：（1）每次只能移动一个盘子；（2）在每根杆子上始终保持大盘在下小盘在上的次序，则需移动盘子最少____次．


    1. A.
      6
    2. B.
      7
    3. C.
      8
    4. D.
      9

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年浙江省杭州市七校联考高二（上）期中数学试卷（解析版） 题型：选择题

    有三根杆子A，B，C，A杆上串有3个穿孔圆盘，尺寸由下到上依次变小，要求按如下规则将圆盘移至C杆上：（1）每次只能移动一个盘子；（2）在每根杆子上始终保持大盘在下小盘在上的次序，则需移动盘子最少（ ）次．
    A．6
    B．7
    C．8
    D．9

    查看答案和解析>>

    同步练习册答案