
设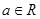 ,函数
,函数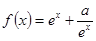 的导函数
的导函数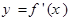 是奇函数,若曲线
是奇函数,若曲线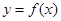 的一条切线的斜率为
的一条切线的斜率为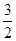 ,则切点的横坐标是( )
,则切点的横坐标是( )
A.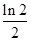 | B. | C.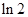 | D.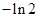 |
科目:高中数学 来源: 题型:单选题
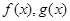 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当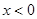 时
时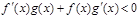 且
且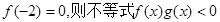 的解集为( )
的解集为( )
| A.(-2,0)∪(2,+∞) |
| B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) |
| D.(-∞,-2)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知f(x)=x2+ax+b,g(x)=x2+cx+d,又f(2x+1)=4g(x),且f′(x)=g′(x),f(5)=30,则g(4)= ( )
A.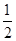 |
B.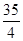 |
C.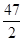 |
D.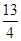 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为k(k>0),贷款的利率为4.8%,假设银行吸收的存款能够全部贷出去.若存款利率为x(x∈(0,0.048)),则银行可获得最大收益时,存款利率为 ( )
| A.0.03 |
| B.0.024 |
| C.0.02 |
| D.0.016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com