
| an+1 |
| an |
| an+1 |
| an |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
| A、{x|x<2} |
| B、{x|x>2} |
| C、{x|o≤x<2} |
| D、{x|0<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| x+2 |
| 30 |
| s |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(元) | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 6 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
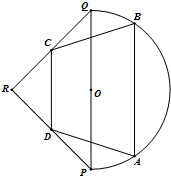 如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.
如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com