练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】定义在[1，＋∞)上的函数f(x)满足：①f(2x)＝2f(x)；②当2≤x≤4时，f(x)＝1－|x－3|.则函数g(x)＝f(x)－2在区间[1,28]上的零点个数为________．

    【答案】4

    【解析】∵定义在[1，＋∞)上的函数f(x)满足：①f(2x)＝2f(x)；②当2≤x≤4时，f(x)＝1－|x－3|，

    ∴函数f(x)在区间[1,28]上的图象如图所示：

    函数g(x)＝f(x)－2在区间[1,28]上的零点个数，即为函数f(x)在区间[1,28]上的图象与直线y＝2交点的个数，由图可得函数f(x)在区间[1,28]上的图象与直线y＝2有4个交点，故函数g(x)＝f(x)－2在区间[1,28]上有4个零点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如下表：

    从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：

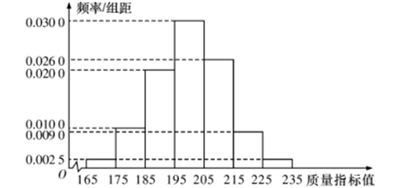
    (1)根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品”的规定？

    (2)在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；

    (3)该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值近似满足，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，（其中， 为自然对数的底数， ……）.

    （1）令，若对任意的恒成立，求实数的值；

    （2）在（1）的条件下，设为整数，且对于任意正整数， ，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点为，上顶点为，直线与直线垂直，椭圆经过点．

    （1）求椭圆的标准方程；

    （2）过点作椭圆的两条互相垂直的弦．若弦的中点分别为，证明：直线恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于集合，定义了一种运算“”，使得集合中的元素间满足条件：如果存在元素，使得对任意，都有，则称元素是集合对运算“”的单位元素．例如： ，运算“”为普通乘法；存在，使得对任意，都有，所以元素是集合对普通乘法的单位元素．

    下面给出三个集合及相应的运算“”：

    ①，运算“”为普通减法；

    ②{表示阶矩阵， }，运算“”为矩阵加法；

    ③（其中是任意非空集合），运算“”为求两个集合的交集．

    其中对运算“”有单位元素的集合序号为（ ）

    A. ①②； B. ①③； C. ①②③； D. ②③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (m,n∈R)在x=1处取得极值2.

    (1)求f(x)的解析式；

    (2)k为何值时，方程f(x)-k=0只有1个根

    (3)设函数g(x)=x2-2ax+a，若对于任意x1∈R，总存在x2∈[-1,0]，使得g(x2)≤f(x1)，求a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， 为圆柱的母线， 是底面圆的直径， 是的中点.

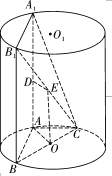
    （Ⅰ）问： 上是否存在点使得平面？请说明理由；

    （Ⅱ）在（Ⅰ）的条件下，若平面，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥外会有被捕的危险，求小鱼被捕的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将圆上每个点的横坐标变为原来的4倍，纵坐标变为原来的3倍，得曲线，以坐标原点为极点， 轴的非负轴分别交于半轴为极轴建立极坐标系，直线的极坐标方程为： ，且直线在直角坐标系中与轴分别交于两点.

    （1）写出曲线的参数方程，直线的普通方程；

    （2）问在曲线上是否存在点，使得的面积，若存在，求出点的坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等式x4＋a1x3＋a2x2＋a3x＋a4＝(x＋1)4＋b1(x＋1)3＋b2(x＋1)2＋b3(x＋1)＋b4，定义映射f：(a1，a2，a3，a4)→(b1，b2，b3，b4)，则f(4,3,2,1)＝(　　)

    A. (1,2,3,4) B. (0,3,4,0)

    C. (0，－3,4，－1) D. (－1,0,2，－2)

    查看答案和解析>>

    同步练习册答案