Question

“城中观海”是近年来国内很多大中型城市内涝所致的现象，究其原因，除天气因素、城市规划等原因外，城市垃圾杂物也是造成内涝的一个重要原因．暴雨会冲刷城市的垃圾杂物一起进入下水道，据统计，在不考虑其它因素的条件下，某段下水道的排水量V（单位：立方米/小时）是杂物垃圾密度x（单位：千克/立方米）的函数．当下水道的垃圾杂物密度达到2千克/立方米时，会造成堵塞，此时排水量为0；当垃圾杂物密度不超过0.2千克/立方米时，排水量是90立方米/小时；研究表明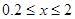，0.2≤x≤2时，排水量V是垃圾杂物密度x的一次函数．
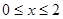（1）当0≤x≤2时，求函数V（x）的表达式；
（2）当垃圾杂物密度x为多大时，垃圾杂物量（单位时间内通过某段下水道的垃圾杂物量，单位：千克/小时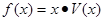）f（x）=x•V（x）可以达到最大，求出这个最大值．

Answer 1

分析：（1）根据题意，对x进行分段求解，当0≤x≤0.2，V（x）=90，当0.2≤x≤2时，利用待定系数法，求出V（x）=-50x+100，最后用分段函数表示出V（x）即可；
（2）表示出f（x）的解析式为分段函数，对0≤x≤0.2上的函数利用单调性求最大值，对0.2≤x≤2上的函数运用基本不等式求最大值，比较两段的最大值，即可得到答案．

解答：解：（1）∵当垃圾杂物密度不超过0.2千克/立方米时，排水量是90立方米/小时，
∴V（x）=90，0≤x≤0.2，
∵0.2≤x≤2时，排水量V是垃圾杂物密度x的一次函数，
∴设为V（x）=mx+n，将（0.2，90），（2，0）代入得：

0.2m+n=90 2m+n=0

，解得m=-50，n=100，
∴V（x）=-50x+100，0.2≤x≤2，
∴

V(x)= 90(0≤x≤0.2) -50x+100(0.2＜x≤2)

；
（2）由题意可得f(x)=x•V(x)=

90x(0≤x≤0.2) -50x(x-2)(0.2＜x≤2)

，
当0≤x≤0.2时，f（x）=90x，最大值为1.8千克/小时，
当0.2≤x≤2时，f（x）=50x（2-x）≤50（x=1时取等号），
∴当杂物垃圾密度x=1千克/立方米，f（x）取得最大值50千克/小时．

点评：本小题主要考查函数模型的选择与应用．解题中考查了待定系数法求函数的解析式，考查了分段函数的解析式以及最值问题．解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．属于中档题．