练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若球的半径为R，则这个球的内接正方体的全面积等于（ ）
    A．8R2
    B．9R2
    C．10R2
    D．12R2
    【答案】分析：球的内接正方体的对角线就是球的直径，求出正方体的棱长，即可求出正方体的表面积．
    解答：解：球的内接正方体的对角线就是球的直径，所以正方体的棱长为：；
    正方体的表面积为：6×=8R2
    故选A．
    点评：本题是基础题，考查球的内接正方体的表面积的求法，本题的关键是正方体的对角线就是球的直径，考查计算能力．解答关键是正方体的对角线和边长的关系．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知ABC的三边长为a，b，c，内切圆半径为r（用S△ABC表示△ABC的面积），则S△ABC=
    12
    r（a+b+c）；类比这一结论有：若三棱锥A-BCD的内切球半径为R，则三棱锥体积VA-BCD=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若△ABC的三边长分别为a、b、c，其内切圆的半径为r，则S△ABC=
    1
    2
    (a+b+c)r    ，类比平几中的这一结论，写出立几中的一个结论为
    若三棱锥A-BCD四个面的面积分别为S1，S2，S3，S4，其内切球的半径为r，则VA-BCD=
    1
    3
    (S1+S2+S3+S4)r
    若三棱锥A-BCD四个面的面积分别为S1，S2，S3，S4，其内切球的半径为r，则VA-BCD=
    1
    3
    (S1+S2+S3+S4)r
    ．

    查看答案和解析>>

    科目：高中数学 来源：2013届河南省周口市高二下学期四校第一次联考文科数学试卷（解析版） 题型：填空题

    在边长分别为a, b, c的三角形ABC中，其内切圆半径为r,则该三角形面积S=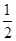(a+b+c)r,将这一结论类比到空间，有“若四面体A—BCD的四个面的面积分别为S，S，S，S，内切球半径为r，则四体的体积”为：         .

     

    查看答案和解析>>

    科目：高中数学 来源：惠州模拟 题型：填空题

    已知ABC的三边长为a，b，c，内切圆半径为r（用S△ABC表示△ABC的面积），则S△ABC=
    1
    2
    r（a+b+c）；类比这一结论有：若三棱锥A-BCD的内切球半径为R，则三棱锥体积VA-BCD=______．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省惠州市高三第三次调研数学试卷（理科）（解析版） 题型：解答题

    已知ABC的三边长为a，b，c，内切圆半径为r（用S△ABC表示△ABC的面积），则S△ABC=r（a+b+c）；类比这一结论有：若三棱锥A-BCD的内切球半径为R，则三棱锥体积VA-BCD=    ．

    查看答案和解析>>

    同步练习册答案