
B.选修4—2 矩阵与变换
已知矩阵
 ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 的变换下得到点
的变换下得到点 ,
,
(1)求实数a的值;
(2)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
|
| π |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:![]() 。
。

B.选修4—2 矩阵与变换
在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系![]() 中,点
中,点![]() 是椭圆
是椭圆![]() 上的一个动点,求
上的一个动点,求![]() 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试数学试题(江苏卷) 题型:解答题
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。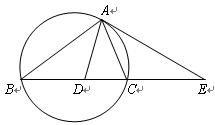 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 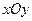 中,设椭圆 中,设椭圆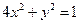 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 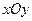 中,点 中,点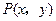 是椭圆 是椭圆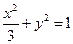 上的一个动点,求 上的一个动点,求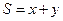 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
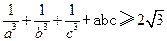 。
。查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试数学试题(江苏卷) 题型:解答题
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证: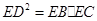 。
。
B.选修4—2 矩阵与变换
在平面直角坐标系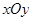 中,设椭圆
中,设椭圆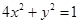 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系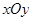 中,点
中,点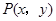 是椭圆
是椭圆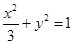 上的一个动点,求
上的一个动点,求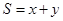 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证: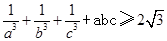 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com