
分析 可以在横线处填入的条件是(1),即“若α∩β=m,n?γ,且α∥γ,n?β,则m∥n”为真命题.如图2所示,由α∩β=m,可得m?β,可得β∩γ=n,已知α∥γ,利用线面平行的性质定理可得m∥n;
在横线处填入的条件不能是(2).如图3所示,即“若α∩β=m,n?γ,且m∥γ,n∥β;则m∥n”为假命题.举反例:假设α∩γ=l,由m∥γ,可得m∥l.若n∩l=P,则m与n必不平行,否则与n∩lP相矛盾;
可以在横线处填入的条件是(3).如图1所示,即“若α∩β=m,n?γ,且m?γ,n∥β,则m∥n”为真命题.利用同一平面内两条直线的位置关系可得m∥n或m∩n=P,由反证法排除m∩n=P即可.
解答 解:可以在横线处填入的条件是(1).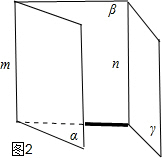
即若α∩β=m,n?γ,且α∥γ,n?β,则m∥n”为真命题.
证明如下:如图2所示,∵α∩β=m,∴m?β,
∵n?γ,n?β,∴β∩γ=n,
又α∥γ,∴m∥n;
在横线处填入的条件不能是(2).
如图3所示,即“若α∩β=m,n?γ,且m∥γ,n∥β;则m∥n”为假命题.
证明:假设α∩γ=l,∵m∥γ,∴m∥l.
若n∩l=P,则m与n必不平行,否则与n∩lP相矛盾;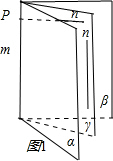
可以在横线处填入的条件是 (3).
即若α∩β=m,n?γ,且m?γ,n∥β,则m∥n”为真命题.
如图1所示,
证明如下:∵α∩β=m,n?γ,m?γ,∴m∥n或m∩n=P,
假设m∩n=P,则P∈n,P∈m,又α∩β=m,∴P∈β,
这与n∥β相矛盾,因此m∩n=P不成立,故m∥n.
故答案为:(1)或(3).
点评 本题考查命题的真假判断与应用,考查空间想象能力和思维能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | 2$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | AC∥平面BA1C1 | B. | AC与平面BA1C1相交 | ||
| C. | AC在平面BA1C1内 | D. | 上述答案均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
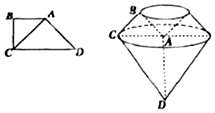 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com