
【题目】如图,已知椭圆的中心在原点,焦点在![]() 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点![]() ,平行于
,平行于![]() 的直线
的直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两个不同点.
两个不同点.

(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数![]() (万人)与沙漠中所需环保车辆数量
(万人)与沙漠中所需环保车辆数量![]() (辆),得到如下统计表:
(辆),得到如下统计表:
参会人数 | 11 | 9 | 8 | 10 | 12 |
所需环保车辆 | 28 | 23 | 20 | 25 | 29 |
(1)根据统计表所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知租用的环保车平均每辆的费用![]() (元)与数量
(元)与数量![]() (辆)的关系为
(辆)的关系为
![]() .主办方根据实际参会人数为所需要投入使用的环保车,
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润![]() 是多少?(注:利润
是多少?(注:利润![]() 主办方支付费用
主办方支付费用![]() 租用车辆的费用).
租用车辆的费用).
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如图数阵的表格形式,表格内是按某种规律排列成的有限个正整数.

(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求
项和,试求![]() 的表达式;
的表达式;
(2)记![]() 为第
为第![]() 行与第
行与第![]() 列交点的数字,观察数阵,若
列交点的数字,观察数阵,若![]() ,试求出
,试求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x∈R|x2-ax+b=0},B={x∈R|x2+cx+15=0},A∩B={3},A∪B={3,5}.
(1)求实数a,b,c的值;
(2)设集合P={x∈R|ax2+bx+c≤7},求集合P∩Z.
查看答案和解析>>
科目:高中数学 来源: 题型:
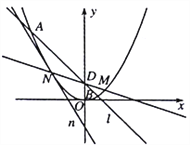
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com