
思路解析:若求an,则需求a1和公比q,这就需要列出关于a1和q的两个方程;另一方面,条件中所给“前n项中数值最大的是54”那么谁是最大的那一项?因此,还要根据公比q的取值来判断这个数列究竟是递增数列、递减数列,还是常数列或摆动数列.
解:∵Sn=80,S2n=6 560,显然公比q≠1,
∴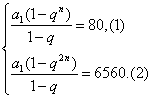
![]() ,得1+qn=82.
,得1+qn=82.
∴qn=81,把它代入(1)中,得![]() =80,即a1=q-1.
=80,即a1=q-1.
而根据条件a1>0,∴q>1.
因此等比数列{an}是递增数列,前n项中数值最大的是an.
∴a1qn-1=54.
又qn=81,∴a1=![]() q.
q.
由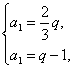 解得a1=2,q=3.
解得a1=2,q=3.
∴an=2·3n-1.
深化升华
解决此题的关键是找出前n项中数值最大的项,这就需要判断数列的单调性.一般地,在等比数列中有a1>0,

a1<0,



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 已知a2010与a2011是首项为正数的等差数列{an}相邻的两项,且函数y=(x-a2010)(x-a2011)的图象如图所示,则使前n项和Sn>0成立的最大自然数n是( )
已知a2010与a2011是首项为正数的等差数列{an}相邻的两项,且函数y=(x-a2010)(x-a2011)的图象如图所示,则使前n项和Sn>0成立的最大自然数n是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市白鹭洲中学高三(上)期中数学试卷(理科)(解析版) 题型:选择题
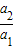 ,
,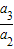 …
…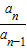 …是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市十校联考高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,
,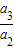 …
… …是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )查看答案和解析>>
科目:高中数学 来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷15(理科)(解析版) 题型:选择题
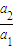 ,
,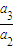 …
…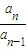 …是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com