
如图,在等腰直角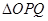 中,
中,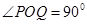 ,
,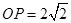 ,点
,点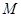 在线段
在线段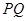 上.
上.
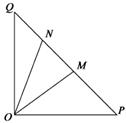
(Ⅰ) 若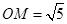 ,求
,求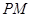 的长;
的长;
(Ⅱ)若点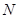 在线段
在线段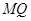 上,且
上,且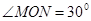 ,问:当
,问:当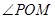 取何值时,
取何值时,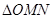 的面积最小?并求出面积的最小值.
的面积最小?并求出面积的最小值.
(Ⅰ) 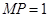 或
或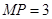 (Ⅱ)当
(Ⅱ)当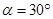 时,
时,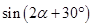 的最大值为
的最大值为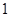 ,此时
,此时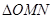 的面积取到最小值.即2
的面积取到最小值.即2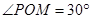 时,
时,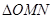 的面积的最小值为
的面积的最小值为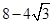
【解析】(Ⅰ)在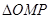 中,
中,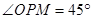 ,
,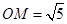 ,
,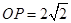 ,
,
由余弦定理得,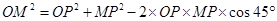 ,
,
得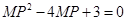 ,
,
解得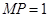 或
或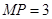 .
.
(Ⅱ)设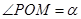 ,
,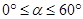 ,
,
在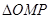 中,由正弦定理,得
中,由正弦定理,得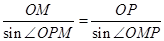 ,
,
所以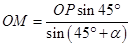 ,
,
同理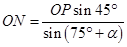
故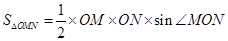
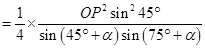
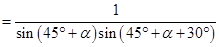
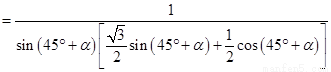

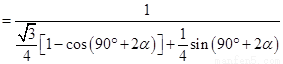

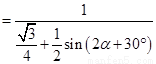
因为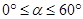 ,
,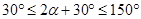 ,所以当
,所以当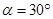 时,
时,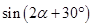 的最大值为
的最大值为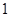 ,此时
,此时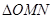 的面积取到最小值.即2
的面积取到最小值.即2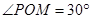 时,
时,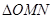 的面积的最小值为
的面积的最小值为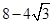 .
.
此题通过正余弦定理巧妙的将面积最值问题通过三角函数呈现,而三角函数的化简过程又比较复杂,但还是有规律可循的,比如差异分析.这就要在平时注意积累,而且计算基本功要硬.
【考点定位】 本题主要考查解三角形、同角三角函数的基本关系、两角和与差的三角函数等基础知识,考查推理论证能力、抽象概括能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思.计算难度比较大,属于难题.


科目:高中数学 来源: 题型:
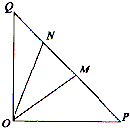 如图,在等腰直角三角形△OPQ中,∠OPQ=90°,OP=2
如图,在等腰直角三角形△OPQ中,∠OPQ=90°,OP=2| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
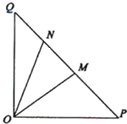 (2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
(2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分 )
如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
, ![]() 为垂足.沿
为垂足.沿![]() 将
将![]() 对折,连结
对折,连结![]() 、
、![]() ,使得
,使得![]() .
.
(1)对折后,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由;
的长;若不存在,说明理由;
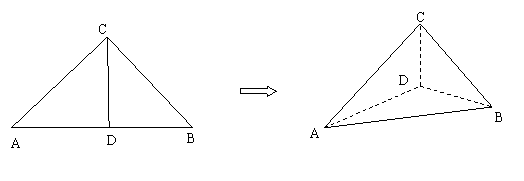 (2)对折后,求二面角
(2)对折后,求二面角![]() 的平面角的大小.
的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com