
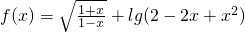 的定义域为M,
的定义域为M,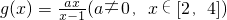 的值域为N.
的值域为N.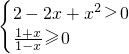 ,解得-1≤x<1,
,解得-1≤x<1,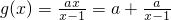 ,
,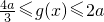 ,所以N∈[
,所以N∈[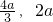 ],又因为M∩N≠∅,可得0<a<
],又因为M∩N≠∅,可得0<a< ,
,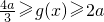 ,所以N=[2a,
,所以N=[2a,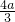 ].
].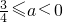 ,
,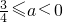 或0<a<
或0<a< }.
}.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:2010-2011学年福建省莆田四中高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 的定义域为M.
的定义域为M.查看答案和解析>>
科目:高中数学 来源:2010年重庆市部分重点中学高考数学一模试卷(理科)(解析版) 题型:解答题
 的定义域为M.
的定义域为M.查看答案和解析>>
科目:高中数学 来源:2010年吉林省高二下学期期末考试理科数学卷 题型:选择题
已知函数 的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则
M∩N=( ) A.{x|x>-1} B.{x|x<1} C.{x|-1<x<1} D.φ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com