
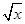 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.科目:高中数学 来源:不详 题型:解答题
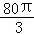 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 -3,x∈[1,2].
-3,x∈[1,2].查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
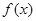 的定义域为
的定义域为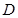 ,如果
,如果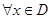 ,存在唯一的
,存在唯一的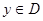 ,使
,使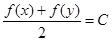 (
(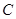 为常数)成立。则称函数
为常数)成立。则称函数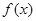 在
在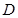 上的“均值”为
上的“均值”为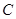 。已知四个函数:
。已知四个函数: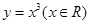 ;②
;②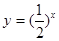
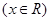 ;③
;③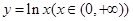 ;④
;④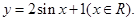
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com