
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
| x+y |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| OA |
| OB |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长郡中学一模文)(13分)在平面直角坐标系中,已知定圆F:![]() (F为圆心),定直线
(F为圆心),定直线![]() ,作与圆F内切且和直线
,作与圆F内切且和直线![]() 相切的动圆P,
相切的动圆P,
(1)试求动圆圆心P的轨迹E的方程。
(2)设过定圆心F的直线![]() 自下而上依次交轨迹E及定园F于点A、B、C、D,
自下而上依次交轨迹E及定园F于点A、B、C、D,
①是否存在直线![]() ,使得
,使得![]() 成立?若存在,请求出这条直线的方程;若不存在,请说明理由。
成立?若存在,请求出这条直线的方程;若不存在,请说明理由。
②当直线![]() 绕点F转动时,
绕点F转动时,![]() 的值是否为定值?若是,请求出这个定值;若不是,请说明理由。
的值是否为定值?若是,请求出这个定值;若不是,请说明理由。

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x+y |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| OA |
| OB |
| OC |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年四川省遂宁市蓬溪中学实验学校高一(下)第二次月考数学试卷(解析版) 题型:解答题
 )=f(x)sinα+(1-sinα)f(y).
)=f(x)sinα+(1-sinα)f(y). ),并在f(
),并在f( )时求出α的值;
)时求出α的值; ),并求出α的值;
),并求出α的值; ,求f(an),并猜测x∈[0,1]时,f(x)的表达式.
,求f(an),并猜测x∈[0,1]时,f(x)的表达式.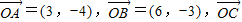 =(5-m,-3-m)
=(5-m,-3-m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com