
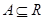 ,如果
,如果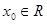 满足:对任意
满足:对任意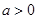 ,都存在
,都存在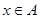 ,使得
,使得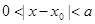 ,那么称
,那么称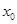 为集合
为集合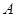 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1)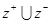 ;(2)
;(2)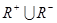 ;(3)
;(3)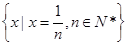 ;(4)
;(4)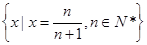 ,以
,以 为聚点的集合有
为聚点的集合有 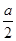 ,(实际上任意比a小得数都可以),使得0<|x|=
,(实际上任意比a小得数都可以),使得0<|x|=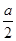 <a,∴0是集合{x|x∈R,x≠0}的聚点;(4)中,集合
<a,∴0是集合{x|x∈R,x≠0}的聚点;(4)中,集合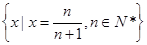 中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大
中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大 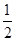 ∴在a<
∴在a<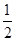 的时候,不存在满足得0<|x|<a的x,∴0不是集合
的时候,不存在满足得0<|x|<a的x,∴0不是集合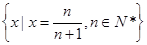 的聚点;(3)集合
的聚点;(3)集合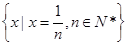 中的元素是极限为0的数列,对于任意的a>0,存在n>
中的元素是极限为0的数列,对于任意的a>0,存在n>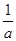 ,使0<|x|=
,使0<|x|=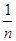 <a,∴0是集合
<a,∴0是集合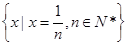 的聚点故答案为(2)(3)
的聚点故答案为(2)(3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com