
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过T(-1,0)作直线与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使△ABE为等边三角形,求x0的值.
解:(1)设M(x,y),P(0,y′),Q(x′,0)(x′>0),
∵![]() =
=![]()
![]() 故由
故由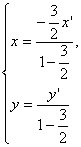 解得
解得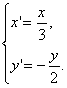 ∴
∴![]()
再由![]() =0,得(6,
=0,得(6,![]() )·(x,
)·(x,![]() y)=0,
y)=0,
6x-![]() y2=0,∴y2=8x(x>0).
y2=0,∴y2=8x(x>0).
故动点M的轨迹C是以(0,0)为顶点、(2,0)为焦点的抛物线(除去原点).
(2)设过T(-1,0)的直线l的方程为y=k(x+1)(k≠0),
代入y2=8x,得k2x2+2(k2-4)x+k2=0.
设A(x1,y1),B(x2,y2),则x1+x2=![]() ,x1x2=1,∴AB中点为(
,x1x2=1,∴AB中点为(![]() ).线段AB的中垂线方程为y
).线段AB的中垂线方程为y![]() ,令y=0,得x0=
,令y=0,得x0=![]() +4=3+
+4=3+![]() .
.
∴E(3+![]() ,0).∵△ABE为等边三角形,故点E到AB的距离为d=
,0).∵△ABE为等边三角形,故点E到AB的距离为d=![]() |AB|.而|AB|=
|AB|.而|AB|=![]() |x2-x1|=
|x2-x1|=![]() ·
·![]() ,
,
故d=![]() .
.
又E到直线y=k(x+1),即kx-y+k=0的距离为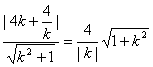 ,
,
由![]() ,解得k=±
,解得k=±![]() .∴3+
.∴3+![]() =6
=6![]() .
.
∴E点坐标为(6![]() ,0).
,0).


科目:高中数学 来源: 题型:
(本小题满分12分)已知点A(2,0),B(0,6),O为坐标原点
(1)若点C在线段OB上,且∠BAC=45°,求△ABC的面积.
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,求P点的坐标。
(3)已知直线L:ax+10y+84-108![]() =0经过P点,求直线L的倾斜角.
=0经过P点,求直线L的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若点C在线段OB上,且∠BAC=![]() ,求△ABC的面积;
,求△ABC的面积;
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,又直线l:ax+10y+84-108![]() =0经过点P,求直线l的倾斜角.
=0经过点P,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源:2013届湖南省高二上学期第三次月考文科数学试卷 题型:解答题
如图,已知点F(2,0),点P在y 轴上运动,过P作PM⊥PF交x轴于M,延长MP到点N,使|PN|=|PM|.
⑵ 求动点N的轨迹C的方程;
⑵在⑴中所求的曲线C上有三点A(x1,y1),B(x2,y2),D(x3,y3),若|AF|、|BF|、|DF|成等差数列,且线段AD的中垂线与x轴的交点为(6,0),求点B的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com