
①f(x)在D上是单调函数;
②存在闭区间[a,b]?D,使f(x)在区间[a,b]上的值域也是[a,b].
那么就称函数y=f(x)为闭函数.
试判断函数y=x2+2x〔x∈[-1,+∞)〕是否为闭函数,如果是闭函数,那么求出符合条件的区间[a,b];如果不是闭函数,请说明理由.
思路分析:本题立意新颖,背景鲜明,设问灵活,体现了考查能力和素质的要求.闭函数的概念是教材上没有的,这类问题的给出可以是新概念、新定理或新规则,其解决策略是先读懂题目,进行信息迁移,获取有用信息,再利用这个新知识作进一步的演算或推理,结合数学知识进而解决问题.先证明函数y=x2+2x〔x∈[-1,+∞)〕是增函数.然后用反证法判断函数y=x2+2x〔x∈[-1,+∞)〕是否为闭函数.
解:设-1≤x1<x2,则有
f(x1)-f(x2)=(x12+2x1)-(x22+2x2)
=(x12-x22)+2(x1-x2)
=(x1-x2)(x1+x2+2),
∵-1≤x1<x2,∴x1-x2<0,x1+x2+2>0.
∴(x1-x2)(x1+x2+2)<0.
∴f(x1)<f(x2).
∴函数y=x2+2x〔x∈[-1,+∞)〕是增函数.
假设存在符合条件的区间[a,b],则有
![]() 即
即 解得
解得![]() 或
或![]() 或
或![]() 或
或![]()
又∵-1≤a<b,∴![]()
∴函数y=x2+2x〔x∈[-1,+∞)〕是闭函数,符合条件的区间是[-1,0].


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
A.“p且q”为真
B.“p或q”为假
C.p真q假
D.p假q真
查看答案和解析>>
科目:高中数学 来源: 题型:
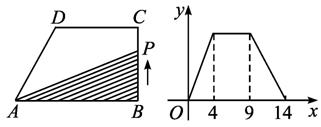
(1) (2)
A.10 B.16 C.18 D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
A.“p且q”为真 B.“p或q”为假
C.p真q假 D.p假q真
查看答案和解析>>
科目:高中数学 来源: 题型:
A.p真q假 B.p假q真
C.“p且q”为真 D.“p或q”为假
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三数学导数及其应用单元练习试卷 题型:填空题
如果函数y=f(x)的导函数的图像如右图所示,给出下列判断:
(1) 函数y=f(x)在区间(3,5)内单调递增;
(2) 函数y=f(x)在区间(-1/2,3)内单调递减;
(3) 函数y=f(x)在区间(-2,2)内单调递增;
|
(5) 当x=2时,函数y=f(x)有极大值;
则上述判断中正确的是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com