Question

函数y=x-lnx的单调递减区间是（ ）
A．（1，+∞）
B．（-∞，1）
C．（0，1）
D．（e，+∞）

Answer 1

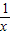
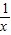
【答案】分析：求出函数的导数为y'=1-，再解y'=1-＜0得x＜1．结合函数的定义域，即可得到单调递减区间是（0，1）
解答：解：函数y=x-lnx的导数为y'=1-
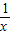
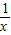
∵令y'=1-＜0，得x＜1
∴结合函数的定义域，得当x∈（0，1）时，函数为单调减函数．
因此，函数y=x-lnx的单调递减区间是（0，1）
故选：C
点评：本题给出含有对数的基本实行函数，求函数的减区间，着重考查了利用导数研究函数的单调性和函数的定义域等知识，属于基础题．