
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:单选题
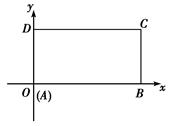
| A.y=-2 | B.y=2,x=5 |
| C.x=5 | D.y=-2,x=5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,“供给—价格”函数的图像为直线
,“供给—价格”函数的图像为直线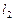 ,它们的斜率分别为
,它们的斜率分别为 ,
, 与
与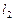 的交点
的交点 为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点
为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点 ,与直线
,与直线 、
、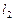 的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点
的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点 的条件为 ( )
的条件为 ( )A. | B. | C. | D. 可取任意实数 可取任意实数 |
 | |||||
 | |||||
 | |||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com