
| 工艺要求 | 立品甲 | 产品乙 | 生产能力/ (台/天) |
| 制白坯时间/天 | 6 | 12 | 120 |
| 油漆时间/天 | 8 | 4 | 64 |
| 单位利润/元 | 20 | 24 | |
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:不详 题型:解答题
 x+10,g(x)=
x+10,g(x)=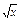 +20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com