
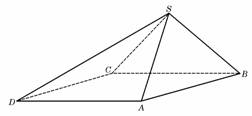
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2![]() ,SA=SB=
,SA=SB=![]() .
.
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.
解法一:(Ⅰ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() .
.
因为![]() ,所以
,所以![]() ,
,
又![]() ,故
,故![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
由三垂线定理,得![]() .
.
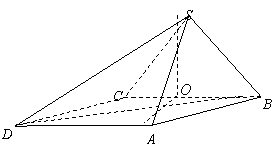 (Ⅱ)由(Ⅰ)知
(Ⅱ)由(Ⅰ)知![]() ,依题设
,依题设![]() ,
,
故![]() ,由
,由![]() ,
,![]() ,
,![]() ,得
,得
![]() ,
,![]() .
.
![]() 的面积
的面积![]() .
.
连结AB,得![]() 的面积
的面积![]()
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由于
,由于![]() ,得
,得
![]() ,
,
解得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
所以,直线![]() 与平面
与平面![]() 所成的我为
所成的我为![]() .
.
解法二:
(Ⅰ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
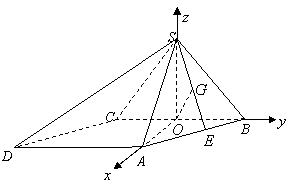 如图,以
如图,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正向,建立直角坐标系
轴正向,建立直角坐标系![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,所以
,所以![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,
,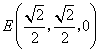 ,
,
连结![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,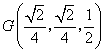 .
.
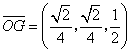 ,
,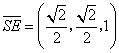 ,
,![]() .
.
![]() ,
,![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() ,
,![]() 垂直.
垂直.
所以![]() 平面
平面![]() ,
,![]() 与
与![]() 的夹角记为
的夹角记为![]() ,
,![]() 与平面
与平面![]() 所成的角记为
所成的角记为![]() ,则
,则![]() 与
与![]() 互余.
互余.
![]() ,
,![]() .
.
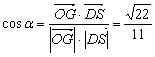 ,
,![]() ,
,
所以,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2015届福建省高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.
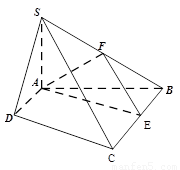
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足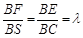 .(
.(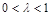 )
)
①求证:对于任意的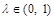 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在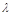 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的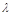 值;若不存在,说明理由.
值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市武昌区高三上学期期末调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在四棱锥S - ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA ="AB=BC" =2,AD =1.M是棱SB的中点.
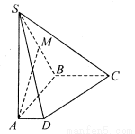
(Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为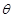 ,求sin
,求sin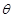 的最大值,
的最大值,
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省高一第三次月考数学试卷 题型:选择题
在正四棱锥S-ABCD中,E是BC的中点,P点在侧面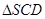 内及其边界上运动,并且总是保持PE
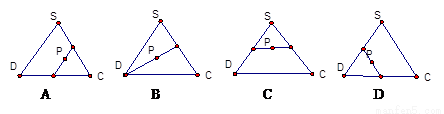
内及其边界上运动,并且总是保持PE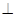 AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是(
).
AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是(
).
查看答案和解析>>
科目:高中数学 来源:2010年龙东南六校高一下学期期末联考数学卷 题型:解答题
(本小题满分10分)如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点。
(Ⅰ)求证:EF∥平面SAD;
(Ⅱ)设SD=2CD,求二面角A-EF-D的正切值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com