练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题

    已知定义在R上的单调函数，当时，，且对任意的实数，∈R，有＝

    (1)

    求；

    (2)

    解：数列满足．

    ①求通项公式的表达式；

    ②当时，不等式对于不小于2的正整数恒成立，求的取值范围

    ③令

    试比较的大小，并加以证明；

    答案：1．赋值法;2．赋值法;
    解析：

    解：令y＝0得f(x)[1－f(0)]＝0，则f(0)＝1………3分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知函数f(x)是定义在R上的偶函数，当x≥0时，f(x)＝－

    (Ⅰ)求当x＜0时，f(x)的解析式；

    (Ⅱ)试确定函数y＝f(x)(x≥0)的单调区间，并证明你的结论；

    (Ⅲ)(理)若x1≥2，且x2≥2

    证明：|f(x1)－f(x2)|＜2．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知二次函数f(x)＝ax2＋bx＋c的图像的顶点坐标是(，－)，且f(3)＝2

    (Ⅰ)求y＝f(x)的表达式，并求出f(1)，f(2)的值；

    (Ⅱ)数列{an}，{bn}，若对任意的实数x都满足g(x)·f(x)＋anx＋bn＝xn+1，n∈N*，其中g(x)是定义在实数R上的一个函数，求数列{an}、{bn}的通项公式；

    (Ⅲ)设圆Cn：(x－an)2＋(y－bn)2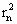＝，若圆Cn与圆Cn+1外切，{rn}是各项都是正数的等比数列，记Sn是前n个圆的面积之和，求．(n∈N*)

    查看答案和解析>>

    科目：高中数学 来源：山东省聊城市2006—2007学年度第一学期高三年级期中考试、数学试题(文科) 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    已知定义在R上奇函数，当x∈(0，1)时，

    (1)

    求f(x)在(－1，1)上的解析式

    (2)

    证明f(x)在(0，1)上是减函数

    查看答案和解析>>

    科目：高中数学 来源：广东省河源市连平县忠信中学2007届高三数学理工农医类11月月考 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤

    已知定义在R上的函数f(x)满足：f(x＋y)＝f(x)－f(y)，当x＜0时，f(x)＜0．

    (1)

    求证：f(x)为奇函数；

    (2)

    求证：f(x)为R上的增函数；

    (3)

    解关于x的不等式：f(ax2)－2f(x)＞f(a2x)－2f(a)(其中a＞0且a为常数)

    查看答案和解析>>

    同步练习册答案