
(本题满分12分)已知二次函数 的最小值为-1,且
的最小值为-1,且 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在
在 上的单调区间与值域.
上的单调区间与值域.
(Ⅰ)a=1, b=-4, c=3;(Ⅱ)[-1,8].
【解析】
试题分析:(Ⅰ)利用待定系数法求二次函数的解析式,根据函数为二次函数,且f(1)=f(3)=0,可以得到函数对称轴x=2,f(x)的最小值为-1,得到顶点坐标,设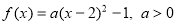 ,不难求解得到a,进而得到函数解析式;
,不难求解得到a,进而得到函数解析式;
(Ⅱ)由(Ⅰ)判断对称轴与区间的位置关系, 不难得到函数的的单调区间,然后求得函数最值,进而得到函数值域.
试题解析:(Ⅰ) ∵ f(x)为二次函数 f(1)=f(3)=0
∴对称轴为x=2
∵二次函数f(x)的最小值为-1,
∴设二次函数的解析式为: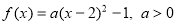 1分
1分
∵f(1)=0 ∴a-1=0 即 a=1 2分
∴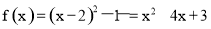 ,
,
故a=1, b=-4, c=3 4分
(Ⅱ)f(x)的单调减区间为:[-1,2],单调增区间为:[2,4] 8分
∴f(x)在x=2处取得最小值为-1, 9分
而f(x)在x=-1处取得最大值为8 10分
故f(x)在[-1,4]上的的值域为:[-1,8] 12分
考点:二次函数在闭区间上的最值;函数解析式的求解及常用方法.


科目:高中数学 来源:2014-2015学年吉林省松原市高一上学期9月月考数学试卷(解析版) 题型:选择题
已知函数 =
= 是定义在[
是定义在[ ]上的偶函数,那么
]上的偶函数,那么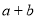 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高一9月阶段考试数学试卷(解析版) 题型:选择题
下列说法中,正确的是( )
A.对任意 ,都有
,都有 ;
;
B. 是
是 上的增函数;
上的增函数;
C.若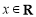 且
且 ,则
,则 ;
;
D.函数y=x|x|是R上的增函数
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省蒙自市高一10月月考数学试卷(解析版) 题型:选择题
函数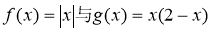 的单调增区间依次为( )
的单调增区间依次为( )
A.(-∞,0] ,[1,+∞) B.(-∞,0],(-∞,1]
C.[0,+∞), [1,+∞) D.[0,+∞),(-∞,1]
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三上学期第二次模拟考试理科数学试卷(解析版) 题型:选择题
把一个四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种不同颜色可供选择,那么不同的染色方法共有( )
A.420种 B.300种 C.360种 D.540种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com