
| 1-x2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| MN |
| MP |
| PM |
| PF |
| AF |
| BF |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).
(2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 1-x2 |
查看答案和解析>>
科目:高中数学 来源:2008年湖北省武汉市武昌区高三元月调考数学试卷(理科)(解析版) 题型:填空题
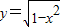 (0≤x≤1)上异于A的点,CD⊥y轴于D,,∠CAO=θ(其中O为原点),将|AC|+|CD|表示成关于θ的函数f(θ),则f(θ)= .
(0≤x≤1)上异于A的点,CD⊥y轴于D,,∠CAO=θ(其中O为原点),将|AC|+|CD|表示成关于θ的函数f(θ),则f(θ)= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com