
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
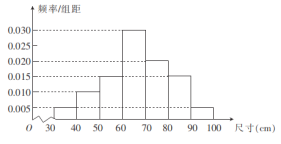
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
【答案】(1)该零件属于“不合格”的零件;(2)![]() .
.
【解析】
(1)先由频率分布直方图中的数据,求出样本平均值,得到![]() ,根据题意,即可得出结果;
,根据题意,即可得出结果;
(2)根据分层抽样的方法得到第一组抽![]() 个,记为
个,记为![]() ;第二组抽
;第二组抽![]() 个,记为
个,记为![]() ,
,![]() ;第三组抽
;第三组抽![]() 个,记为
个,记为![]() ,
,![]() ,
,![]() ,用列举法列举出总的基本事件,以及满足条件的基本事件,进而可得出结果.
,用列举法列举出总的基本事件,以及满足条件的基本事件,进而可得出结果.
(1)由频率分布直方图可得,该批零件的样本平均值为:
![]()
![]() ;
;
则![]() ,
,![]() ,
,![]() ,
,
所以该零件属于“不合格”的零件;
(2)按照分层抽样抽![]() 个零件时,第一组抽
个零件时,第一组抽![]() 个,记为
个,记为![]() ;第二组抽
;第二组抽![]() 个,记为
个,记为![]() ,
,![]() ;第三组抽
;第三组抽![]() 个,记为
个,记为![]() ,
,![]() ,
,![]() ,
,
从这![]() 个零件中抽取
个零件中抽取![]() 个零件共有
个零件共有![]() 种情况,分别为
种情况,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中再抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的有
的有![]() 种,分别为
种,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据古典概型概率公式,可得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
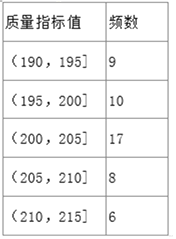
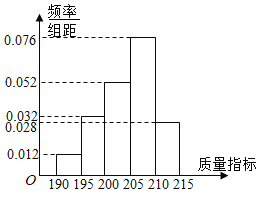
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com