练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    把1、2、3、4、5这五个数字组成无重复数字的五位数，并把它们按由小到大的顺序排列成一个数列.

    （1）       43251是这个数列的第几项？

    （2）       这个数列的第96项是多少？

    （3）       求这个数列的各项和.


    解：⑴先考虑大于43251的数，分为以下三类

                   第一类：以5打头的有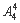： =24

                   第二类：以45打头的有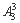： =6

                   第三类：以435打头的有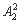： =2………………………………2分

    故不大于43251的五位数有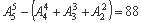：（个）

    即43251是第88项.…………………………………………………………………4分

    ⑵数列共有A=120项，96项以后还有120-96=24项，

    即比96项所表示的五位数大的五位数有24个，

    所以小于以5打头的五位数中最大的一个就是该数列的第96项.即为45321.…8分

    ⑶因为1，2，3，4，5各在万位上时都有A个五位数，所以万位上数字的和为：（1+2+3+4+5）·A·10000……………………………………………………………10分

    同理它们在千位、十位、个位上也都有A个五位数，所以这个数列各项和为：

    （1+2+3+4+5）·A·（1+10+100+1000+10000）

    =15×24×11111=3999960……………………………………………………………12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    把平面上一切单位向量归结到共同的始点，那么这些向量的终点

    所构成的图形是___________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···，第n个三角形数为。记第n个k边形数为N(n,k)(),以下列出了部分k边形数中第n个数的表达式：

    三角形数   N(n,3)=            正方形数   N(n,4)=

    五边形数   N(n,5)=            六边形数   N(n,6)=

    可以推测N(n,k)的表达式，由此计算N(10,24)= ____________

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列满足，则（  ）

      A. 0          B.  　        C.             D. 6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用二项式定理计算9.985，精确到1的近似值为(   )

     A.99000　   B.99002　　  C.99004　　　 D.99005

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数（ ）

    A．－1          B．        C．  D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知sin α＝，则cos4α的值是(　　)

    A. B．－ C. D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数 则 是 成立的  （   ）

    A .充分不必要条件   B .必要不充分条件    C .充要条件     D .既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    把化为二进制的数是（    ）．

    　A．　　　 　 B．　　　　　 C．　 　 D．

    查看答案和解析>>

    同步练习册答案