
有一解三角形的题目,因纸张破损有一个条件丢失,具体如下:在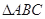 中,已知
中,已知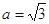 ,
, , ,求角
, ,求角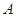 .经推断,破损处的条件为三角形的一边长度,且答案为
.经推断,破损处的条件为三角形的一边长度,且答案为 .将条件补充完整填在空白处.
.将条件补充完整填在空白处.
【解析】
试题分析:因为 ,所以∴1+cos(A+C)=(
,所以∴1+cos(A+C)=( -1)cosB,即1-cosB=(
-1)cosB,即1-cosB=(
-1)cosB,整理得cosB= 又∵0°<B<180°,∴B=45°.接下来分两种情况讨论:
又∵0°<B<180°,∴B=45°.接下来分两种情况讨论:
(1)当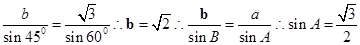 又因为A∈(0,π),且a>b,所以A="60°" 或者A=120°,这与已知角A的解为唯一解矛盾
又因为A∈(0,π),且a>b,所以A="60°" 或者A=120°,这与已知角A的解为唯一解矛盾
(2) B=45°,结合A=60°,得C=75°,则由正弦定理可知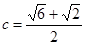 ,再由
,再由 又∵A∈(0,π),且c>a,∴A=60°,且此解是唯一解,符合题意,故可知
又∵A∈(0,π),且c>a,∴A=60°,且此解是唯一解,符合题意,故可知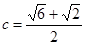
考点:解三角形
点评:本题给出三角形一边和一角,探索三角形有唯一解的问题,着重考查了运用正、余弦定理解三角形和三角恒等变换等知识,属于中档题.


科目:高中数学 来源: 题型:
| 3 |
| A+C |
| 2 |
| 2 |
| ||||
| 2 |
| ||||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com