
分析 可得:分母为1的有2项;分母为2的有4项;分母为3的有6项;…,分母为n的有2n项;可得:从分母为1到分母为n的所有项的总数为:2+4+…+2n=n2+n.分别令n=44,n=45,即可判断出结论.其中第2016个分数是分母为45的第36个,为$\frac{18}{45}$.
解答 解:一列数是这样排列的:$\frac{1}{1}$,$\frac{1}{1}$,$\frac{1}{2}$,$\frac{1}{2}$,$\frac{2}{2}$,$\frac{2}{2}$,$\frac{1}{3}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{2}{3}$,$\frac{3}{3}$,$\frac{3}{3}$…,
可得:分母为1的有2项;分母为2的有4项;分母为3的有6项;…,分母为n的有2n项;
∴从分母为1到分母为n的所有项的总数为:2+4+…+2n=2×$\frac{n(1+n)}{2}$=n2+n.
令n=44,则442+44=1980;
令n=45,则452+45=2070.
∴其中第2016个分数是分母为45的第36个,为$\frac{18}{45}$.
故答案为:$\frac{18}{45}$.
点评 本题考查了数列的通项公式、等差数列的求和公式,考查了观察分析猜想归纳推理能力与计算能力,属于中档题.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>$\sqrt{7}$-2 | B. | 0<a<$\sqrt{7}$-2 | C. | a≥$\sqrt{7}$-2 | D. | 0<a≤$\sqrt{7}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 9种 | C. | 3种 | D. | 26种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
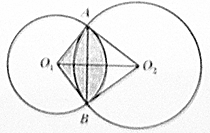 如图,已知圆O1与O2相交于A、B两点,△AO2B为正三角形,|AO2|=2$\sqrt{3}$,且|O1O2|=4,则阴影部分的面积为( )
如图,已知圆O1与O2相交于A、B两点,△AO2B为正三角形,|AO2|=2$\sqrt{3}$,且|O1O2|=4,则阴影部分的面积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com