分析:由已知中四面体DABC的体积为
,
∠ACB=,AD=1,BC+=2,我们可以设四棱锥D-ABC的高为DA',结合点到平面的距离垂线段最短,我们可以构造一个不等式,结合基本不等式,我们易判断出AD与平面ABC垂直,并且可以求出BC及AC的长,结合勾股定理即可得到答案.
解答:解:已知如下图所示:
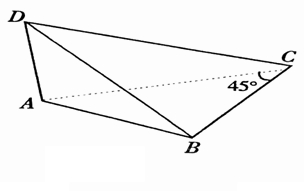
作DA'⊥平面ABC,则AD≥A'D
则V
D-ABC=
•A′D(•AC•BC•sin45°)=
≤
•AD(•AC•BC•sin45°)即
AD•BC•≥1
由基本不等式得AD+
BC+≥3
≥3
当且仅当AD=BC=
=1时取等号,
而AD+
BC+=2+1=3
故AD'=AD=1
即AD⊥平面ABC
此时,AC=
,
由勾股定理易得CD=
故答案为:
点评:本题考查的知识点是棱锥的体积及直线与平面垂直的性质,其中根据已知条件,结合基本不等式判断出AD与平面ABC垂直,是解答本题的关键.



