
(本小题满分18分)设数列{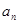 }的前
}的前 项和为
项和为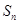 ,且满足
,且满足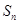 =2-
=2-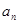 ,(
,( =1,2,3,…)
=1,2,3,…)
(Ⅰ)求数列{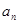 }的通项公式;
}的通项公式;
(Ⅱ)若数列{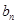 }满足
}满足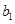 =1,且
=1,且 ,求数列{
,求数列{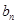 }的通项公式;
}的通项公式;
(Ⅲ)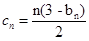 ,求
,求 的前
的前 项和
项和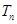
(Ⅰ) an=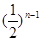 (n∈N*); (Ⅱ) bn=3-2(
(n∈N*); (Ⅱ) bn=3-2( )n-; (Ⅲ)
)n-; (Ⅲ) 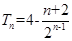 。
。
【解析】
试题分析:(Ⅰ)∵n=1时,a1+S1=a1+a1=2
∴a1=1
∵Sn=2-an即an+Sn=2 ∴an+1+Sn+1=2
两式相减:an+1-an+Sn+1-Sn=0
即an+1-an+an+1=0,故有2an+1=an
∵an≠0 ∴ (n∈N*)
(n∈N*)
所以,数列{an}为首项a1=1,公比为 的等比数列.an=
的等比数列.an=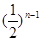 (n∈N*)
(n∈N*)
(Ⅱ)∵bn+1=bn+an(n=1,2,3,…)
∴bn+1-bn=( )n-1
)n-1
得b2-b1=1
b3-b2=
b4-b3=( )2
)2
……
bn-bn-1=( )n-2(n=2,3,…)
)n-2(n=2,3,…)
将这n-1个等式相加,得
bn-b1=1+
又∵b1=1,∴bn=3-2( )n-1(n=1,2,3,…)
)n-1(n=1,2,3,…)
(3)
所以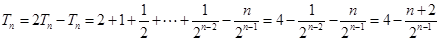
考点:数列通项公式的求法;数列前n项和的求法。
点评:若已知递推公式为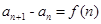 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若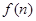 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若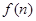 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③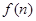 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④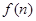 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。


科目:高中数学 来源: 题型:
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成![]() 个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为
个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为![]() 。求
。求
(Ⅰ)![]() ;
;
(Ⅱ)![]() 与
与![]() 的关系式;
的关系式;
(Ⅲ)数列![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分18分)已知数列{an}、{bn}、{cn}的通项公式满足bn=an+1-an,cn=bn+1-bn(n∈N*?),若数列{bn}是一个非零常数列,则称数列{an}是一阶等差数列;若数列{cn}是一个非零常数列,则称数列{an}是二阶等差数列?(1)试写出满足条件a1=1,b1=1,cn=1(n∈N*?)的二阶等差数列{an}的前五项;(2)求满足条件(1)的二阶等差数列{an}的通项公式an;(3)若数列{an}首项a1=2,且满足cn-bn+1+3an=-2n+1(n∈N*?),求数列{an}的通项公式
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com