
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为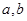 .
.
(Ⅰ)求直线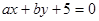 与圆
与圆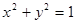 有公共点的概率;
有公共点的概率;
(Ⅱ)求方程组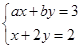 只有正数解的概率。
只有正数解的概率。
(Ⅰ) (Ⅱ)P(方程组只有正数解)=
(Ⅱ)P(方程组只有正数解)=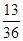
【解析】(Ⅰ)直线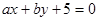 与圆
与圆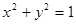 有公共点的概率则圆心到直线的距离
小于半径,即
有公共点的概率则圆心到直线的距离
小于半径,即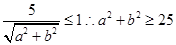 ,列出a,b的符合条件的情况,古典概型求解;
,列出a,b的符合条件的情况,古典概型求解;
方程组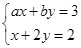 ,的解为正,则
,的解为正,则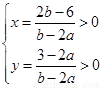 ,求出a,b的范围,列出即可。
,求出a,b的范围,列出即可。
解:(Ⅰ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
因为直线ax+by+5=0与圆x2+y2=1有公共点,所以有
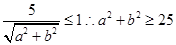 ,由于a,b∈{1,2,3,4,5,6}.
,由于a,b∈{1,2,3,4,5,6}.
∵满足条件 <25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.
<25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.
所以,直线ax+by+c=0与圆x2+y2=1有公共点的概率是 ---6分
---6分
(Ⅱ)由方程组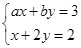 ,得
,得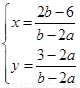
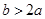 时,
时, ,即
,即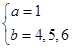 符合条件的数组
符合条件的数组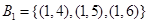 共有3个
共有3个
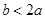 时,
时,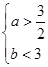 ,即
,即 符合条件的数组
符合条件的数组
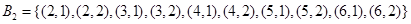 共有10个
共有10个
故P(方程组只有正数解)=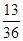


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com