
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是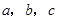 ,已知
,已知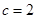 ,
,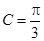 .(I)若
.(I)若 的面积等于
的面积等于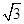 ,求
,求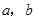 ;(II)若
;(II)若 ,求
,求 的面积.
的面积.
(Ⅰ) (Ⅱ)
(Ⅱ)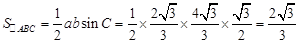 。
。
【解析】此题考查了正弦定理,余弦定理,和差化积公式,二倍角的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值,其中正弦定理及余弦定理很好的解决了三角形的边角关系,熟练掌握定理及公式是解本题的关键.
(I)由C的度数求出sinC和cosC的值,利用余弦定理表示出c2,把c和cosC的值代入得到一个关于a与b的关系式,再由sinC的值及三角形的面积等于
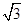 ,利用面积公式列出a与b的另一个关系式,两个关系式联立即可即可求出a与b的值;
,利用面积公式列出a与b的另一个关系式,两个关系式联立即可即可求出a与b的值;
(II)由sinB=2sinA,再利用正弦定理化简得到b=2a,与第一问中余弦定理得到的a与b的关系式联立,求出a与b的值,综上,由求出的a与b的值得到ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
解:(Ⅰ)由题意,得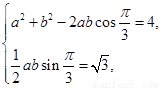 即
即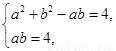 ………6分
………6分
因为 所以
所以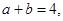
由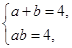 得
得 …………………………………………6分
…………………………………………6分
(Ⅱ)由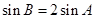 得,
得, . …………………………………………7分
. …………………………………………7分
由余弦定理得, ,
,
∴ 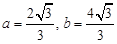 .
…………………………………………10分
.
…………………………………………10分
∴ 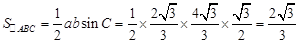 ………………………12分
………………………12分


科目:高中数学 来源:2014届山东冠县武训高中高二上学期10月月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
.
(1)若 的面积等于
的面积等于 ,求
,求 ;
;
(2)若 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二第二学期5月月考文科数学 题型:解答题
(本小题满分15分)
在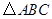 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .(Ⅰ)若
.(Ⅰ)若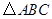 的面积等于
的面积等于 ,求
,求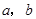 ;
;
(Ⅱ)若 ,求
,求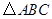 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com