
 是奇函数(a>0且a≠1)
是奇函数(a>0且a≠1)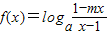 是奇函数(a>0且a≠1),
是奇函数(a>0且a≠1),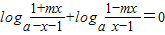 ,即
,即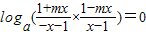 ,
, ,即1-m2x2=1-x2,∴m2=1,解得m=±1.
,即1-m2x2=1-x2,∴m2=1,解得m=±1.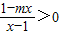 ,∴m=1应舍去.
,∴m=1应舍去. ,其定义域为{x|x<-1,或x>1}关于原点对称,故适合.
,其定义域为{x|x<-1,或x>1}关于原点对称,故适合.
 =
=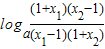
 ,又a>1,
,又a>1,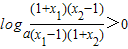


科目:高中数学 来源: 题型:解答题
 是奇函数(a∈R).
是奇函数(a∈R).查看答案和解析>>
科目:高中数学 来源:四川省期中题 题型:解答题
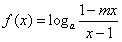 是奇函数(a>0, 且a≠1)。
是奇函数(a>0, 且a≠1)。查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省淮安市清江中学高一(上)期末数学试卷(解析版) 题型:解答题
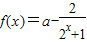 是奇函数(a∈R).
是奇函数(a∈R).查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区高考数学二模试卷(文科)(解析版) 题型:解答题
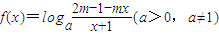 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com