
设点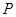 是双曲线
是双曲线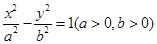 与圆
与圆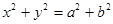 在第一象限的交点,其中
在第一象限的交点,其中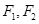 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且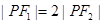 ,则双曲线的离心率为
,则双曲线的离心率为
A.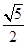 | B.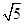 | C.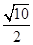 | D. |
B
解析考点:双曲线的简单性质.
专题:计算题.
分析:由P是双曲线 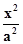 -
- 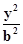 =1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,推导出∠F1PF2=90°.再由|PF1|=2|PF2|,知|PF1|=4a,|PF2|=2a,由此求出c=
=1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,推导出∠F1PF2=90°.再由|PF1|=2|PF2|,知|PF1|=4a,|PF2|=2a,由此求出c= 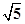 a,从而得到双曲线的离心率.
a,从而得到双曲线的离心率.
解答:解:∵P是双曲线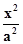 -
-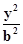 =1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,
=1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,
∴点P到原点的距离|PO|=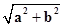 =c,
=c,
∴∠F1PF2=90°,
∵|PF1|=2|PF2|,
∴|PF1|-|PF2|=|PF2|=2a,∴|PF1|=4a,|PF2|=2a,
∴16a2+4a2=4c2,
∴c=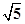 a,
a,
∴e=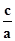 =
=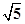 .
.
故选B.
点评:本题考查双曲线的性质和应用,解题时要注意公式的灵活运用.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com