练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    焦点在轴上的椭圆的一个顶点为，右焦点到直线的距离为3.

    （1）求椭圆的方程；

    （2）是否存在斜率为的直线与椭圆交于两点，使得？若存在，求出的取值范围；若不存在，请说出理由.

    答案(1)；（2）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知中心在坐标原点，焦点在坐标轴上的椭圆G与x轴交于A、C两点，与y轴交于B、D两点，且A点的坐标为（-2，0），四边形ABCD的面积为4．
    （1）求椭圆G的方程；
    （2）过x轴上一点M（1，0）作一条不垂直于y轴的直线l，交椭圆G于E、F点，是否存在直线l，使得△AEF的面积为
    		7
    ，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2014届广东省高二上学期期末考试文科数学试卷（解析版） 题型：填空题

     设是三角形的一个内角，且，则方程表示的曲线是焦点 在  _轴上的__ （填抛物线、椭圆、双曲线的一种）

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012年福建省四地六校高二第二次月考理科数学 题型：解答题

    (本题满分13分)

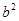    把一颗骰子投掷两次，记第一次出现的点数为，第二次出现的点数为（其中）．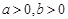

    （Ⅰ）若记事件“焦点在轴上的椭圆的方程为”，求事件的概率；

    （Ⅱ）若记事件“离心率为2的双曲线的方程为”，求事件的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2013届福建省漳州市高二上学期期末考试理科数学试卷 题型：解答题

    已知中心在原点，焦点在x轴的椭圆的离心率为，椭圆上一点P到两个焦点的距离之和为8，

    （1）求椭圆的方程

    （2）求与上述椭圆共焦点，且一条渐近线为y=x的双曲线方程

     

    查看答案和解析>>

    科目：高中数学 来源：2013届福建省高二上学期期末考试理科数学试卷 题型：解答题

    把一颗骰子投掷两次，记第一次出现的点数为，第二次出现的点数为（其中）．

    （Ⅰ）若记事件“焦点在轴上的椭圆的方程为”，求事件的概率；

    （Ⅱ）若记事件“离心率为2的双曲线的方程为”，求事件的概率．

     

    查看答案和解析>>

    同步练习册答案