
(2007
北京,16)如下图,在Rt△AOB中,∠OAB=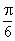 ,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.动点D在斜边AB上.
(1)
求证:平面COD⊥平面AOB;(2)
当D为AB的中点时,求异面直线AO与CD所成角的大小;(3)
求CD与平面AOB所成角的最大值.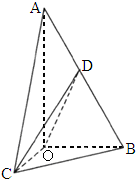
|
解析: (1)由题意,CO⊥AO,BO⊥AO,∴∠ BOC是二面角B-AO-C的平面角.又∵二面角 B-AO-C是直二面角,∴CO⊥BO,又∵AO∩BO=0,∴ CO⊥平面AOB,又 CO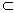 平面COD, 平面COD,
∴平面 COD⊥平面AOB.(2) 作DE⊥OB,垂足为E,连结CE(如下图),则DE∥AO,∴∠CDE是异面直线AO与CD所成的角.
在 Rt△COE中,CO=BO=2,OE=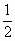 BO=1,∴CE= BO=1,∴CE=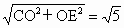 . .
又 DE=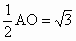 ,∴在Rt△CDE中,tan∠CDE= ,∴在Rt△CDE中,tan∠CDE=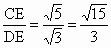 , ,
∴异面直线 AO与CD所成角的大小为 . .
(3) 由(1)知,CO⊥平面AOB,∴∠ CDO是CD与平面AOB所成的角,且 tan∠CDO=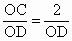 .当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D, .当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,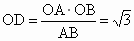 , ,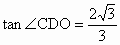 , ,
∴ CD与平面AOB所成角的最大值为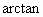 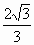 . . |
|
剖析:本题考查立体几何的旋转问题和异面直线所成的角,以及空间想象能力和逻辑推理能力. |


科目:高中数学 来源: 题型:013
(2007
北京西城模拟)在1,2,3,4,5这五个数字所组成的没有重复数字的三位数中,其各个数字之和为9的三位数共有[
]|
A .16个 |
B .18个 |
C .19个 |
D .21个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com