
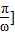 上的函数y=Asin2ωx(A>0)与直线y=2有且只有一个公共点,且截直线y=1所得的弦长为2,则ω= .
上的函数y=Asin2ωx(A>0)与直线y=2有且只有一个公共点,且截直线y=1所得的弦长为2,则ω= . 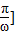 上的交点为M(x1,
上的交点为M(x1, ),N(x2,
),N(x2, ),再根据题意得出x2-x1=2,2ωx2=
),再根据题意得出x2-x1=2,2ωx2=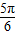 ,2ωx1=
,2ωx1=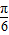 ,问题即可解决.
,问题即可解决.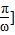 上的交点为M(x1,
上的交点为M(x1, ),N(x2,
),N(x2, ),
), ,x∈[0,
,x∈[0,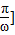 ,
,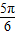 ,2ωx1=
,2ωx1=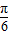 ,
,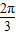 ,
,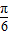 .
.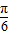 .
. ),N(x2,
),N(x2, )后,结论2ωx2=
)后,结论2ωx2=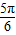 ,2ωx1=
,2ωx1=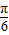 的分析与应用,属于中档题.
的分析与应用,属于中档题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
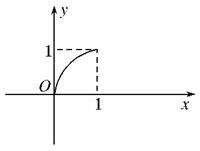
①f(x2)-f(x1)>x2-x1;
②x2f(x1)>x1f(x2);
③![]() <f
<f![]() .
.
其中正确结论的序号是___: _____.(把所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省黄冈市中学高二(下)期末数学试卷(文科)(解析版) 题型:选择题
 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com