
 D,使得平面BC
D,使得平面BC D
D 平面ABD.
平面ABD.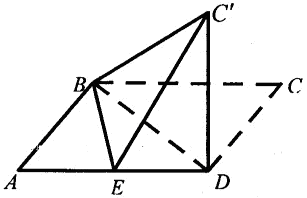
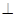 平面ABD;
平面ABD;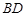 与平面
与平面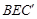 所成角的正弦值为
所成角的正弦值为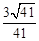 .
. 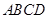 中,
中,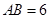 ,
,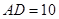 ,
,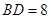 ,
,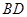 将△
将△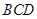 翻折成△
翻折成△ 后
后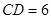 ,
, ,
,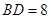 ,
,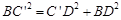 ,得
,得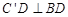 .再根据平面
.再根据平面 ⊥平面
⊥平面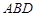 ,平面
,平面
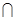 平面
平面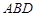 即得证;
即得证;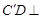 平面
平面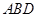 ,且
,且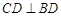 ,因此,可以
,因此,可以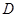 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系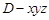 .
.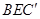 法向量为
法向量为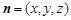 ,
,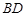 与平面
与平面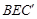 所成角为
所成角为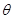 ,即得所求.
,即得所求. 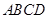 中,
中,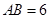 ,
,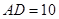 ,
,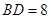 ,
,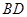 将△
将△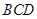 翻折成△
翻折成△
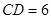 ,
, ,
,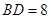 ,
,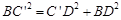 ,
,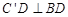 . 2分
. 2分 ⊥平面
⊥平面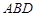 ,平面
,平面
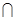 平面
平面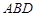 ,
,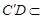 平面
平面 ,∴
,∴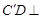 平面
平面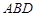 . 5分
. 5分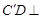 平面
平面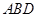 ,且
,且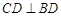 ,
,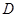 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系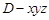 . 6分
. 6分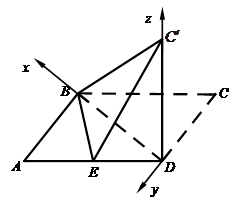
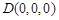 ,
,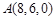 ,
,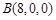 ,
,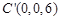 .
.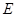 是线段
是线段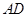 的中点,
的中点,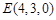 ,
,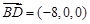 .
.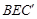 中,
中,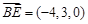 ,
,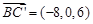 ,
,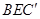 法向量为
法向量为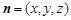 ,
,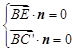 ,即
,即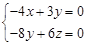 ,
,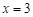 ,得
,得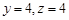 ,故
,故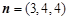 . 9分
. 9分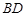 与平面
与平面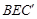 所成角为
所成角为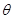 ,则
,则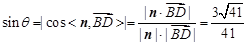 . 11分
. 11分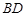 与平面
与平面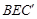 所成角的正弦值为
所成角的正弦值为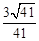 . 12分
. 12分

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
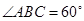 ,平面
,平面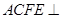 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.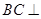 平面ACFE;
平面ACFE;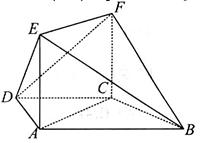
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
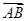 ,b=
,b=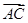 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.n1=(1,2,1),n2=(-3,1,1) |
| B.n1=(1,1,2),n2=(-2,1,1) |
| C.n1=(1,1,1),n2=(-1,2,1) |
| D.n1=(1,2,1),n2=(0,-2,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com