
| ||
| 3 |
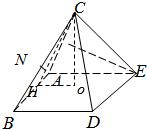 解:设AB=2,作CO⊥面ABDE,
解:设AB=2,作CO⊥面ABDE,| 3 |
| 3 |
| AN |
| 1 |
| 2 |
| AC |
| AB |
| EM |
| 1 |
| 2 |
| AC |
| AE |
| AN |
| EM |
| 1 |
| 2 |
| AB |
. |
| AC |
| 1 |
| 2 |
| AC |
| AE |
| 1 |
| 2 |
| ||||
|
|
| 1 |
| 6 |
| 1 |
| 6 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A |
| 2 |
| π |
| 4 |
| B |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省卫辉市高三2月月考数学理卷 题型:选择题
下列命题中不正确命题的个数是( )
①经过空间一点一定可作一平面与两异面直线都平行;
②已知平面 、
、 ,直线a、b,若
,直线a、b,若 ,
, ,则
,则 ;
;
③有两个侧面垂直于底面的四棱柱为直四棱柱;
④四个侧面两两全等的四棱柱为直四棱柱;
⑤底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
⑥底面是等边三角形,∠APB=∠BPC=∠CPA,则三棱锥P-ABC是正三棱锥.
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com