分析:(Ⅰ)直接利用直线与平面平行的判定定理证明AB1∥面BDC1;
(Ⅱ)通过等体积的方法,求解点A1到面BDC1的距离即可.
解答:解:(Ⅰ)证明:连接B
1C,交BC
1于点O,则O为B
1C
的中点,∵D为AC中点∴OD∥A B
1又∵A B
1?平面BDC
1,OD?平面BDC
1∴A B
1∥平面BDC
1-----------------------(6分)
(Ⅱ)在直角三角形BDC中过点C作BD的垂线,垂足为E,连接C
1E.
∵AA
1⊥平面ABC,AA
1∥CC
1∴CC
1⊥平面ABC 又∵BD?平面ABC∴CC
1⊥BD
∴BD⊥平面C
1CE∴BD⊥C
1E
在Rt△CBD中,BD=
=
,CE=
=
在Rt△C
1CE中,C1E=
=
=
---------(10分)
∵
V三棱锥B-A1DC1=V三棱锥A1-BDC1设点A
1到面BDC
1的距离为h,则有
S△C1BD•h=S△A1DC1•BC所以h=
=
---------(12分)
点评:本题考查直线与平面平行的判定定理,点到平面的距离的距离的求法,等体积的应用,考查逻辑推理能力与计算能力,转化思想的应用.

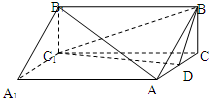 (2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
(2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
