
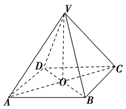
 如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积. 分析 连AC、BD相交于点O,连VO,求出VO,则VV-ABCD=$\frac{1}{3}$SABCD•VO,由此能求出这个正四棱锥的体积.
解答 解:连AC、BD相交于点O,连VO,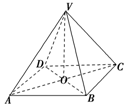 ∵AB=BC=2 cm,
∵AB=BC=2 cm,
∴在正方形ABCD中,CO=$\sqrt{2}$ cm,
在直角三角形VOC中,VO=$\sqrt{14}$ cm,
∴VV-ABCD=$\frac{1}{3}$SABCD•VO=$\frac{1}{3}$×4×$\sqrt{14}$=$\frac{4}{3}$$\sqrt{14}$(cm3).
故这个正四棱锥的体积为$\frac{4}{3}$$\sqrt{14}$ cm3.
点评 本题考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
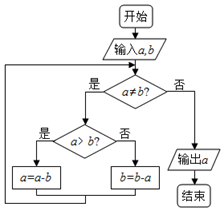 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为63,98,则输出的a=( )| A. | 9 | B. | 3 | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | (2,3) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p,q均为真命题 | |
| B. | “a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 | |
| C. | 在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 | |
| D. | 命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com