
 ,
, ),斜率为
),斜率为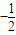 的直线上;
的直线上; }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.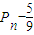 }是首项为
}是首项为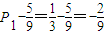 ,公比为
,公比为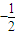 的等比数列,即可求数列的通项;
的等比数列,即可求数列的通项;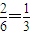 ,
,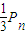 .…(3分)
.…(3分) ,
,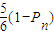 .
.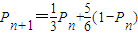 ,变形得
,变形得 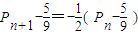 .
. ,
, ),斜率为
),斜率为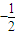 的直线上.…(6分)
的直线上.…(6分)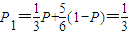 ,
,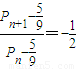 ,
, }是首项为
}是首项为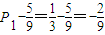 ,公比为
,公比为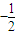 的等比数列,…(8分)
的等比数列,…(8分)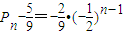 ,
,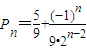 .…(10分)
.…(10分)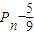 }是首项为
}是首项为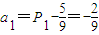 ,公比为
,公比为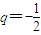 的等比数列,又
的等比数列,又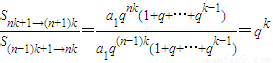 (k∈N*)是常数,
(k∈N*)是常数,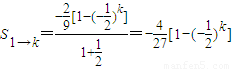
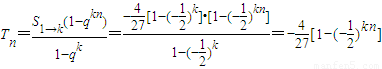 .…(14分)
.…(14分)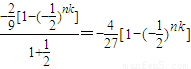 .…(14分)
.…(14分)

科目:高中数学 来源: 题型:
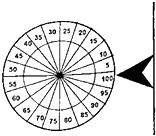 中央二台经济生活频道,在主持人马斌主持的“购物街”栏目中,有一个幸运转盘游戏该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲、乙两名入选观众每人都有两次转动盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记;且规定:若某人在第一次转动后,认为分值理想,则可以放弃第二次机会,得分按第一次所指的数记,两人中得分多者为优胜,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85,试回答以下问题:
中央二台经济生活频道,在主持人马斌主持的“购物街”栏目中,有一个幸运转盘游戏该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲、乙两名入选观众每人都有两次转动盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记;且规定:若某人在第一次转动后,认为分值理想,则可以放弃第二次机会,得分按第一次所指的数记,两人中得分多者为优胜,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85,试回答以下问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
查看答案和解析>>
科目:高中数学 来源:湛江二模 题型:解答题
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
| 5 |
| 9 |
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
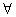 n∈N*,点(Pn,Pn+1)恒在过定点
n∈N*,点(Pn,Pn+1)恒在过定点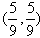 斜率为-
斜率为-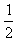 的直线上;
的直线上;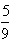 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…S(n-1)k+1→nk的前n项和Tn。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com