
| A.恰有1名男生与恰有2名女生 |
| B.至少有1名男生与全是男生 |
| C.至少有1名男生与至少有1名女生 |
| D.至少有1名男生与全是女生 |
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:不详 题型:解答题
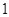 小时收费
小时收费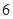 元,超过
元,超过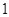 小时的部分每小时收费
小时的部分每小时收费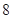 元(不足
元(不足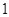 小时的部分按
小时的部分按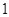 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过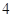 小时.
小时.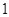 小时以上且不超过
小时以上且不超过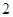 小时的概率为
小时的概率为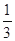 ,停车付费多于
,停车付费多于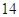 元的概率为
元的概率为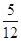 ,求甲停车付费恰为
,求甲停车付费恰为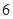 元的概率;
元的概率;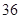 元的概率.
元的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1/1000 | B.1/100 | C.1/10 | D.1/9 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
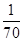 ”,根据这位负责人的话可以推断出参加面试的人数为( ).
”,根据这位负责人的话可以推断出参加面试的人数为( ).| A.20 | B.21 | C.10 | D.70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
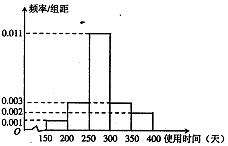
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com