
思路解析:用随机模拟的方法可以估算点落在圆内的概率,由几何概率公式可得点落在圆内的概率为![]() ,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
解:(1)利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND;
(2)进行平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2,得到两组[-1,1]上的均匀随机数;
(3)统计试验总次数N和落在阴影内的点数N1(满足条件a2+b2≤1的点(a,b)的个数);
(4)计算频率![]() ,即为点落在圆内的概率的近似值;
,即为点落在圆内的概率的近似值;
(5)设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=![]() .
.
∴![]() =
=![]() .
.
∴S≈![]() ,即为圆的面积的近似值.
,即为圆的面积的近似值.
又S圆=πr2=π,∴π=S≈![]() ,即为圆周率的近似值.
,即为圆周率的近似值.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如图3-3,某人投标投中圆的概率是多少(投在正方形外面或边缘不算)?
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.
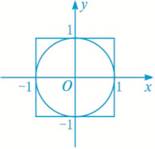
图3-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com