首项为正的等差数列{an}的前n项和为Sn(n∈N*),且a2011a2012<0,a2011+a2012>0,使Sn>0成立的n的最大值为( )
A.4020
B.4021
C.4022
D.4023
【答案】
分析:由题意可得a
2011>0,a
2012 <0,a
2011>|a
2012|,可得 a
1+a
4022=a
2011+a
2012>0,a
1+a
4023=a
2011+a
2013 =2a
2012 <0,再等差数列的前n项和公式可得
S
4022>0,S
4023<0,由此得到结论.
解答:解:∵首项为正的等差数列{a
n}的前n项和为S
n(n∈N
*),且a
2011a
2012<0,a
2011+a
2012>0,
∴a
2011>0,a
2012 <0,a
2011>|a
2012|,
∴a
1+a
4022=a
2011+a
2012>0,a
1+a
4023=a
2011+a
2013 =2a
2012 <0.
∴S
4022=
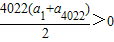
,S
4023=
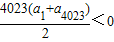
,
故使S
n>0成立的n的最大值为 4022,
故选C.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,等差数列的前n项和公式的应用,属于中档题.

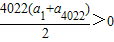 ,S4023=
,S4023=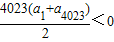 ,
,

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案