
(1)已知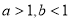 ,求证:
,求证: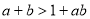 ;
;
(2)已知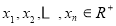 ,且
,且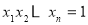 ,
,
求证: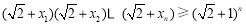 .
.
证明见解析.
【解析】
试题分析:(1)本题证明只要利用作差法即可证得;(2)这个不等式比较复杂,考虑到不等式的形式,我们可用数学归纳法证明,关键在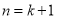 时的命题如何应用
时的命题如何应用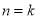 时的结论,
时的结论,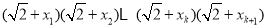 中要把两个括号合并成一个,又能应用
中要把两个括号合并成一个,又能应用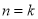 时的结论证明
时的结论证明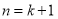 时的结论,当
时的结论,当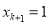 时,结论已经成立,当
时,结论已经成立,当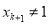 时,在
时,在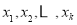 中可找到一个,不妨设为
中可找到一个,不妨设为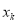 ,使
,使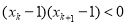 ,即
,即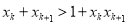 ,从而有
,从而有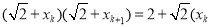
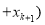
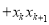
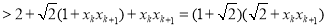 ,这样代入进去可证得
,这样代入进去可证得 时结论成立.
时结论成立.
(1)因为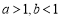 ,所以
,所以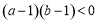 ,即
,即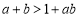 ; 2分
; 2分
(2)证法一(数学归纳法):(ⅰ)当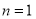 时,
时,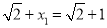 ,不等式成立. 4分
,不等式成立. 4分
(ⅱ)假设 时不等式成立,即
时不等式成立,即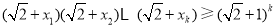 成立. 5分
成立. 5分
则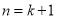 时,若
时,若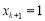 ,则命题成立;若
,则命题成立;若 ,则
,则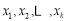 中必存在一个数小于1,不妨设这个数为
中必存在一个数小于1,不妨设这个数为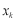 ,从而
,从而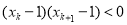 ,即
,即 .
.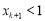 同理可得,
同理可得,
所以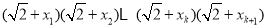
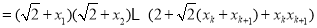
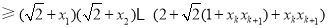
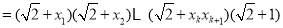
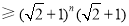
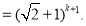
故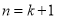 时,不等式也成立. 9分
时,不等式也成立. 9分
由(ⅰ)(ⅱ)及数学归纳法原理知原不等式成立. 10分
证法二:(恒等展开)左右展开,得
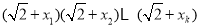
 由平均值不等式,得
由平均值不等式,得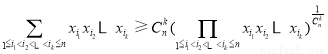
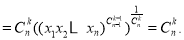 8分
8分
故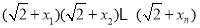
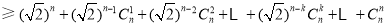
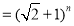 . 10分
. 10分
考点:(1)比较法证不等式;(2)数学归纳法证不等式.


科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:解答题
已知函数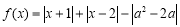 ,若函数
,若函数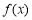 的图象恒在
的图象恒在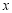 轴上方,求实数
轴上方,求实数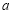 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:填空题
设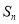 为数列
为数列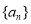 的前
的前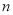 项和,
项和,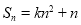 ,
,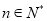 ,其中
,其中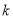 是常数.若对于任意的
是常数.若对于任意的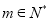 ,
,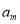 ,
,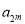 ,
,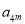 成等比数列,则
成等比数列,则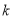 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:填空题
某工厂甲、乙、丙三个车间生产同一产品,数量分别为120件,90件,60
件. 为了解它们的产品质量是否有显著差异,用分层抽样方法抽取了一个容量
为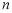 的样本进行调查,其中从丙车间的产品中抽取了4件,则
的样本进行调查,其中从丙车间的产品中抽取了4件,则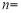 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷理科数学试卷(解析版) 题型:解答题
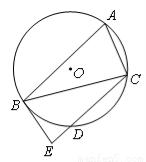
如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是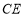 与⊙O的交点.若
与⊙O的交点.若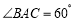 ,
,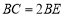 ,求证:
,求证: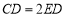 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷理科数学试卷(解析版) 题型:填空题
已知数列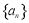 是各项均不为
是各项均不为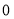 的等差数列,
的等差数列,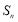 为其前
为其前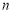 项和,且满足
项和,且满足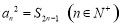 .若不等式
.若不等式 对任意的
对任意的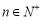 恒成立,则实数
恒成立,则实数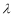 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷文科数学试卷(解析版) 题型:解答题
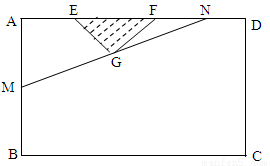
某小区想利用一矩形空地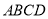 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且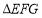 中,
中,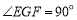 ,经测量得到
,经测量得到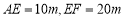 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点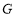 作一直线交
作一直线交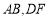 于
于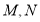 ,从而得到五边形
,从而得到五边形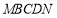 的市民健身广场,设
的市民健身广场,设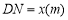 .
.
(1)将五边形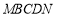 的面积
的面积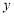 表示为
表示为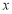 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:解答题
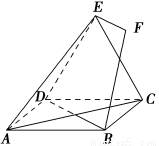
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=EF.
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com